Models and Simulations | Ion Channels | Cardiac Cells | Cardiac Tissue
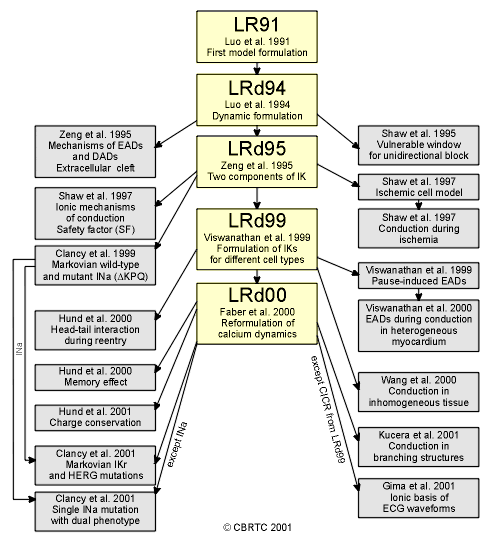
LR91 (1991) | LRd94 (1994) | LRd95 (1995) | LRd99 (1999) | LRd00 (2000) | LRd07 (2007)
LR91:
Luo C.H., Rudy Y. A model of the ventricular cardiac action potential. Depolarization, repolarization, and their interaction. Circ Res 68:1501-26, 1991
First formulation by Luo and Rudy, inspired by Beeler & Reuter (1977).
The model implements six transmembrane currents and, like the Beeler-Reuter model, takes into account concentration changes of intracellular Ca2+ only.
The transmembrane currents are:
INa : Na+ inward current. Formulation according to Beeler & Reuter, with modifications proposed by Haas et al. (1971) and Ebihara & Johnson (1980), with adjustments.
Isi: Slow (Ca2+ ) inward current. Formulation of Beeler & Reuter.
IK: Time-dependent K+ current (delayed rectifier). Formulation of Beeler & Reuter, with modifications.
IKp: Plateau K+ current. Original formulation.
Ib: Background current.Original formulation.
LRd94: (“d” indicates “dynamic”)
Luo C.H., Rudy Y. A dynamic model of the cardiac ventricular action potential. I. Simulations of ionic currents and concentration changes. Circ Res 74:1071-96, 1994
Luo C.H. Rudy, Y. A dynamic model of the cardiac ventricular action potential. II. Afterdepolarizations, triggered activity, and potentiation. Circ Res 74:1097-113, 1994
Major extension of the LR91 model. Serves as a basis for all subsequent studies. Includes formulation for most of the sarcolemmal currents, pumps and exchangers. Implements cell compartmentalization (myoplasm, junctional and nonjunctional sarcoplasmic reticulum), Ca2+ buffers in the myoplasm (troponin, calmodulin) and in the junctional sarcoplasmic reticulum (calsequestrin), and calcium-inducedCa2+ release. It takes into account myoplasmic concentration changes of Na+ and K+ as well as Ca2+ concentration changes in all three compartments. Sarcolemmal currents are normalized to cell membrane capacitance and expressed in µA/µF, not in µA/cm2 (as in LR91 and Beeler-Reuter models). In the initial work, Ca2+ buffering was computed using Steffensen’s iterative method. Later, buffering was computed analytically (see LRd95 ).
Sarcolemmal currents:
Currents from LR91 and specific changes:
INa: Reduction of gNamax from 23 mS/cm2 to 16 mS/µF.
ICa,L: L-type Ca2+ inward current. Replaces I si (which becomes obsolete) used in LR91 . Original new formulation. Note erratum below .
IK: Square-dependence on activation gate x was incorporated.
IK1: gK1 max at [K+]o = 5.4 mmol/L was increased from 0.6047 mS/cm2 to 0.75 mS/µF.
IKp: No changes
Ib: Replaced by INa,b and ICa,b (see “New currents” below) and therefore becomes obsolete.
New currents:
INaCa: Na+ /Ca2+ exchanger current. Formulation according to Di Francesco & Noble (1985), with adjustments.
INaK: Na+ /K+ ATPase current. Original formulation, inspired by Di Francesco & Noble (1985) and Rasmusson et al. (1990) .
IpCa: Ca2+ pump. Original formulation.
ICa,b: Ca2+ background current. Together with INa,b , replaces Ib from LR91 , which becomes obsolete. Original formulation.
INa,b: Na+ background current. Together with ICa,b , replaces Ib from LR91 , which becomes obsolete. Original formulation.
Intracellular calcium fluxes:
Irel,CICR: Ca2+ -induced Ca2+ release (CICR) from the junctional sarcoplasmic reticulum (JSR). Original formulation. Triggered by Ca2+ entry during 2 ms starting from the time of occurrence of dV/dtmax . CICR is graded (increases with increasing Ca2+ entry) but involves a threshold (no release for small entry of Ca2+ , below a given threshold) .
Iup: Ca2+ uptake into the nonjunctional sarcoplasmic reticulum (NSR). Original formulation.
Ileak: Ca2+ leakage from the NSR. Original formulation.
Itr: Translocation of Ca2+ from the NSR to the JSR. Original formulation.
Processes specifically used to model pathophysiological conditions (not used in other studies unless explicitely stated):
Used to model cell behavior under Ca2+-overload conditions (resting diastolic
[Ca2+] myoplasmic,free >0.3 µmol/L):
Ins(Ca): Non specific Ca2+-activated sarcolemmal current. Original formulation.
Irel,spont: Spontaneous Ca2+ release from the JSR . Original formulation. Triggered by a level of buffered Ca2+ in the JSR exceeding a given threshold.
LRd95:
Zeng J., Laurita K.R., Rosenbaum D.S., Rudy Y. Two components of the delayed rectifier K+ current in ventricular myocytes of the guinea pig type. Theoretical formulation and their role in repolarization. Circ Res 77:140-52, 1995
Incorporation of the two components (rapid and slow) of the delayed rectifier K+ current. Introduction of an analytical method to compute Ca2+ buffering (based on solving polynomial equations of 2nd and 3rd degrees), replacing Steffensen’s iterative method used in LRd94 .
Specific changes compared with LRd94:
IK: IK from LRd94 is replaced with IKr and IKs (see “New currents” below) and therefore becomes obsolete.
IKp: gKpmax decreased from 0.0183 to 0.00552 mS/µF.
ICa,L: Hill coefficient (exponent) in gate fCa changed from 2 to 1.
New currents:
IKr: Rapid component of the delayed rectifier K+ current. Original formulation. Maximal conductance is [K+]o -dependent.
IKs: Slow component of the delayed rectifier K+ current. Original formulation. Maximal conductance is Ca2+ -dependent.
ICa,T: T-type Ca2+ current. Original formulation.
LRd99:
Viswanathan P.C., Shaw R.M., Rudy Y. Effects of IKr and IKs heterogeneity on action potential duration and its rate dependence: a simulation study. Circulation 99:2466-74, 1999
Refinement of IKs , CICR (graded release without threshold) and formulation for three different cell types: epi-, mid- and endocardial. The default model cell (control), used in subsequent studies, is epicardial unless stated otherwise.
Specific changes compared with LRd95 (for the control epicardial cell):
IKs : Incorporation of a second xs gate ( xs2 ). The first xs gate ( xs1 ) is the same as the xs gate in LRd95 . Reformulation of gKsmax and its Ca2+ -dependence.
Irel,CICR : Reformulation of Grel by adding a cubic tail to its initial formulation which involved a threshold (no CICR at all for a small entry of Ca2+ ). With this formulation, CICR always occurs (graded response even for a small entry of Ca2+ ).
Unpublished changes:
INaK: Change of INa,Kmax from 1.5 to 2 µA/µF and of Hill exponent from 1.5 to 2.
INa,b: Increase of gNa,bmax from 0.00141 to 0.004 mS/µF.
Specific formulation for mid- and endocardial cells:
IKs : In the control epicardial cell, the scaling constant of gKsmax is 0.433. To model mid- and endocardial cells, this constant is changed to 0.125 and 0.289, respectively. This models an IKs density ratio of about 23:7:15 (exactly: 0.433:0.125:0.289) in epi-/mid-/endocardial cells.
LRd00:
Faber G.M., Rudy Y. Action potential and contractility changes in [Na(+)](i) overloaded cardiac myocytes: a simulation study. Biophys J 78:2392-404, 2000
Reformulation of CICR and INaCa. Formulation of the Na+-activated K+ current, used to model cell behavior under Na+ overload conditions.
A sample source program code (in C/C++) can be found online.
Specific changes compared with LRd99:
INaCa: Reformulation according to Varghese & Sell (1997).
INaK: Increase of INa,Kmax from 2 to 2.25 µA/µF.
Iup: Iupmax increased from 0.005 to 0.00875 mmol/L/ms.
Irel,CICR: Original reformulation. Triggered by Ca2+ entry starting from the time of occurrence of dV/dtmax. CICR is graded, without threshold.
Processes specifically used to model pathophysiological conditions (not used in other studies unless explicitely stated):
Used to model cell behavior under Na+ -overload conditions ([Na+ ]i >10 mmol/L):
IK(Na) : Na+ -activated K+ current. Original formulation.
How to calculate changes in [Ca 2+]i:
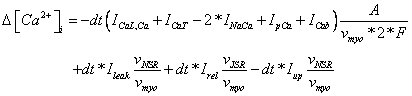
Livshitz L.M., Rudy Y. Regulation of Ca2+ and electrical alternans in cardiac myocytes: role of CaMKII and repolarizing currents. Am J Physiol Heart Circ Physiol 292:H2854-H2866, 2007
Livshitz and Rudy modified LRd, incorporating new findings in the relationship between Ca-transient, ICa(L) and SR Ca loading. This version of LRd shows AP and Ca-transient alternans at very fast pacing.
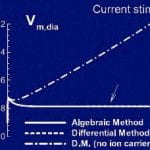
2009 L. Livshitz, Y. Rudy “Uniqueness and Stability of Action Potential Models during Rest, Pacing, and Conduction Using Problem-Solving Environment“. 2009, Biophysical J, 97(5) pp. 1265 – 1276 Download: Matlab code Development and application of physiologically detailed dynamic models of the action potential (AP) and Ca 2+ cycling in cardiac cells is a rapidly growing aspect of computational cardiac electrophysiology. Given the large scale of the nonlinear system involved, questions were recently raised regarding reproducibility, numerical stability, and uniqueness of model solutions, as well as ability of the model to simulate AP propagation in multicellular configurations. To address these issues, we reexamined ventricular models of myocyte AP developed in our laboratory with the following results. 1), Recognizing that the model involves a system of differential-algebraic equations, a procedure is developed for estimating consistent initial conditions that insure uniqueness and stability of the solution. 2), Model parameters that can be used to modify these initial conditions according to experimental values are identified. 3), A convergence criterion for steady-state solution is defined based on tracking the incremental contribution of each ion species to the membrane voltage. 4), Singularities in state variable formulations are removed analytically. 5), A biphasic current stimulus is implemented to completely eliminate stimulus artifact during long-term pacing over a broad range of frequencies. 6), Using the AP computed based on 1? above, an efficient scheme is developed for computing propagation in multicellular models.  Click to Enlarge
Click to Enlarge
2001 Hund, T. J., J. P. Kucera, et al. (2001). “Ionic charge conservation and long-term steady state in the Luo-Rudy dynamic cell model.” Biophys J 81(6): 3324-31. It has been reported in the literature that dynamic cell models, which account for changes in intracellular ion concentrations, show a nonphysiological drift in computed parameters (Yehia et al., 1999; Endresen et al., 2000; Rappel, 2001). This drift occurs during rapid pacing for prolonged periods of time (Yehia et al., 1999; Rappel, 2001). The results of the present study establish that such drift is due to a nonconservative implementation of the stimulus, and not to an intrinsic property of the LRd model. The drift disappears when ions carried by the stimulus current are accounted for in the computation of ion concentrations. In general, when using a dynamic model, any source of charge (such as the stimulus) must also be considered a source of ions. Failure to do so violates conservation and may produce a nonphysiological behavior due to drift of model parameters. In this study, the problem is easily corrected by incorporating the stimulus current into the total K+ current in the LRd formulation. Assuming that other ions in the system (Na+ and Ca2+) to be the stimulus charge carrier is also consistent with the conservation principle, as long as these ions are accounted for in the formulation.
1999 Viswanathan, P. C. and Y. Rudy (1999). “Pause induced early afterdepolarizations in the long QT syndrome: a simulation study.” Cardiovasc Res 42(2): 530-42. The long QT syndrome (LQTS) is characterized by prolonged repolarization and propensity to syncope and sudden death due to polymorphic ventricular tachycardias such as torsade de pointes (TdP). The exact mechanism of TdP is unclear, but pause-induced early afterdepolarizations (EADs) have been implicated in its initiation. In this study we investigate the mechanism of pause-induced EADs following pacing at clinically relevant rates and characterize the sensitivity of different cell types (epicardial, midmyocardial, and endocardial) to EAD development. Simulations were conducted using the Luo-Rudy (LRd) model of the mamalian ventricular action potential (AP).
1997 Shaw, R. M. and Y. Rudy (1997). “Electrophysiologic effects of acute myocardial ischemia: a theoretical study of altered cell excitability and action potential duration.” Cardiovasc Res 35(2): 256-72. To study the ionic mechanisms of electrophysiologic changes in cell excitability and action potential duration during the acute phase of myocardial ischemia. Using an ionic-based theoretical model of the cardiac ventricular cell, the dynamic LRd model, we have simulated the three major component conditions of acute ischemia (elevated [K]o, acidosis and anoxia) at the level of individual ionic currents and ionic concentrations. The conditions were applied individually and in combination to identify ionic mechanisms responsible for reduced excitability at rest potentials, delayed recovery of excitability, and shortened action potential duration.  Click to Enlarge
Click to Enlarge
ICa,L (LRd94 , Luo and Rudy, 1994):
In Circ Res 74:1071-96, 1994, the equation for the steady-state of activation gate f of ICa,L is erroneous. The correct equation is in Circ Res 74:1097-113, 1994.
IK(ATP) (Shaw and Rudy, 1997):
In Cardiovasc Res 35:256-72, 1997, k0.5 (k1/2 ) in the equation for PATP should be 0.250 µmol/L, not 0.250 mmol/L. The correct value is in Circ Res 80:124-38, 1997.
Markovian INa (Clancy and Rudy, 1999):
In Nature, 400:566-9, 1999, some equations for the rate constants are erroneous.
(Viswanathan, Shaw and Rudy,1999): GKr and GKs conductances are mismatched in the legend to Fig. 2A. To reproduce figure 2A, GKr should be 0.028 and GKs should be 0.65.
IK(Na) (LRd00 , Faber and Rudy, 2000):
In Biophys J, 78:2392-404, 2000, the unit for gK(Na)max should be µS/µF, not µS/cm2.
Irel (LRd00 , Faber and Rudy, 2000):
In Biophys J, 78:2392-404, 2000, the value for t should be set to zero at the time of dICa,total/dtmax, not dV/dtmax.
 Click to Enlarge
Click to Enlarge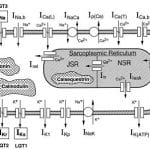 Click to Enlarge
Click to Enlarge